Use this to select different options to be used in an All Subsets Regression – Generalized Linear Models analysis.
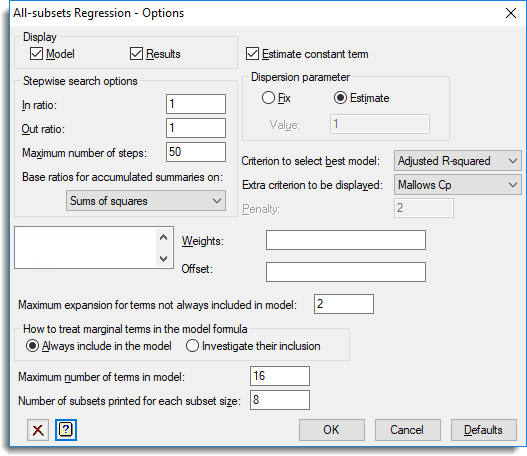
Display
Specifies which items of output are to be displayed in the Output window.
| Model | Details of the model |
| Results | Results from the analysis |
Estimate constant term
Specifies whether to include a constant in the model.
Dispersion parameter
Controls whether the dispersion parameter for the variance of the response is estimated from the residual mean square of the fitted model, or fixed at a given value. The dispersion parameter (fixed or estimated) is used when calculating standard errors and standardized residuals. In models with the binomial, Poisson, negative binomial, geometric and exponential distributions, the dispersion should be fixed at 1 unless a heterogeneity parameter is to be estimated.
Stepwise search options
Options specific to the stepwise search methods
In ratio
Specifies the criterion for inclusion of terms for forward selection, backward elimination and stepwise regression.
Out ratio
Specifies the criterion for exclusion of terms for forward selection, backward elimination and stepwise regression.
Maximum number of steps
Specifies the limit on the number of times to repeat stepwise selection methods, unless no change is made.
Base ratios for accumulated summaries on:
Lets you specify the way in which variance ratios are calculated in accumulated analysis of deviance summaries. You can choose either to use Sums of squares or Mean sums of squares.
Criterion to use to select best model:
Lets you select the criterion to use for selecting best models among all possible models. The criteria employed are defined as follows:
| R-squared | 100 x [1 – Dev / Dev0] |
| Adjusted R-squared | 100 x [1 – (Dev / (n-p)) / (Dev0 / (n-p0))] |
| Mallow’s Cp | Dev / f + 2 x p – n |
| Ep | Dev x (n+1) x (n-2) / [n x (n-p) x (n-p-1)] |
| Akaike information | Dev / f + 2 x p |
| Schwarz information | Dev / f + ln(n) x p |
| Deviance | Dev |
| Mean deviance | Dev / (n-p) |
where
| Dev | Is the deviance of the current model |
| Dev0 | Is the deviance of the null model |
| p | Is the number of fitted parameters of the current model |
| p0 | Is the number of fitted parameters of the null model |
| n | Is the number of units |
| f | Is the dispersion parameter |
The null model is the model with only a constant term, which may include the fitting of a grouping factor for a within groups regression and/or the fitting of cut-points for an ordinal response model.
Extra criterion to be displayed
Lets you select an extra criterion which is also displayed in the Output Window for the selected best models
Penalty
Specifies the penalty used for Mallow’s Cp and Akaike’s Information Criterion.
Weights
A variate of weights can be supplied to give varying influence of each unit on the fit of the model.
Offset
Specifies a variate that can be used to take account of a fixed contribution to the linear effects for each unit, referred to as the offset.
Maximum expansion for terms not always included in model
This can be used to limit the expansion of the model terms for the fitting of all possible regression models. The expansion is limited in addition to the limitation imposed by the Factorial option on the main dialog.
How to treat marginal terms in the model formula
This controls how marginal terms (e.g. the interaction A.B is marginal to the main effects of A and B) are handled in the models that are tried:
| Always include in the model | The models tried will always contain marginal terms. |
| Investigate their inclusion | The models tried will include dropping marginal terms. If a model fails the marginality requirements, an entry marg will be printed in the table of probabilities. |
Maximum number of terms in model
The lets you specify the maximum number of candidate terms in a model. This can be used when only models with few candidate terms are relevant or to reduce the computational burden. For example with 12 candidate terms there are 4096 different models, while there are only 299 models with maximally three terms. Specifying a maximum of 3 terms then saves a considerable amount of computing time.
Number of subsets printed for each subset size
Specifies the number of best models within each subset size for which summary statistics are printed.