Multiple Comparisons for Predictions is available via the Predictions from General Linear Regression and Predictions from Generalized Linear Model dialogs for General Linear and Generalized Linear regression models respectively, but only if the option Show Multiple Comparisons in menus has been enabled on the Tools | Options | Menus tab. It is only available for predictions from one or more factors that gives at least 3 predictions and where only a single value of a variate in the model is used. Further, in the Generalized Linear models, it is only available if the Back Transform none option is selected.
Multiple comparison tests are designed to take account of the fact that there may be many possible comparisons between pairs of treatment predictions in a regression analysis (with n treatments there are n (n-1) / 2). So, some researchers feel that their significance levels should be adjusted to take account of all the tests that they might make – and this can be achieved by use of a multiple comparison test.
Conversely, it has been pointed out that multiple comparisons are unnecessary if you have only a small number of comparisons to make – either because there are few treatments, or because you should have identified beforehand the comparisons that you feel are likely to be of interest. Also, they are inappropriate if the treatments have any sort of structure. For example, the levels of a treatment factor may represent different amounts of a substance like a fertiliser or a drug. It would then be more sensible to assess the treatment effect over all its levels by fitting some sort of trend, and implausible to assume that only some of the amounts might have an effect. Alternatively, the treatments may have a factorial structure, and you should then be more interested in studying the main effects and interactions of the various factors. For further discussion of the issues see Nelder (1971), Maindonald and Cox (1984) and Perry (1986).
The methodology implemented here closely follows that described in Chapter 5 of Hsu (1996).
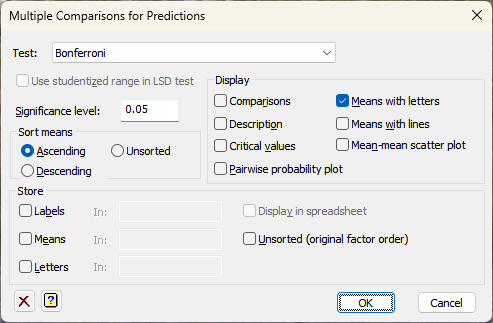
Test
This lets you select the type of multiple comparison tests to be performed. The following choices are available in the current version of Genstat:
| Fisher’s Unprotected LSD |
| Bonferroni |
| Sidak |
Please see the references below for a full technical description of the methods used when calculating these statistics.
Use studentized range test in LSD test
If the Fisher’s Protected Least Significant Difference or the Fisher’s Unprotected Least Significant Difference test are selected, the LSD test uses the Studentized Range statistic rather than Student’s t (for further information see Hsu, 1996, page 139).
Sort means
Lets you arrange the means in either Ascending or Descending order.
Significance level
Specifies the experiment-wise significance level for the intervals. You must enter a number between 0 and 1 (Default 0.05).
Display
Specifies which items of output are to be produced.
| Comparisons | The differences between the pair of means, upper and lower confidence limits for the differences, t-statistics and an indication of whether or not they are significant. |
| Description | Description including information such as the experiment-wise and compartment-wise error rates. |
| Critical values | Gives critical values for the t-statistic for situations where these do not vary amongst the comparisons (i.e. for the Scheffe, Bonferroni and Sidak methods, as well as the Fisher LSD methods, provided all the comparisons have the same number of residual degrees of freedom). |
| Pairwise probability plot | The probabilities of differences between means displayed in a shade plot. |
| Means with letters | The means, with identical letters (a, b etc.) alongside those that do not differ significantly. |
| Means with lines | The means, with lines joining those that do not differ significantly. |
| Mean-mean scatter plot | Produces a mean-mean scatter plot (see Hsu 1996, pages 151-153). |
Store
Specifies which items of output are to be saved. After selecting the appropriate boxes, you need to type the names for the identifiers of the data structures into the corresponding In: fields. The results will be in the order specified in the Sort means option.
| Labels | The labels for the predicted means. |
| Means | The predicted mean values. |
| Letters | Letters indicating which means are significantly different. |
Display in spreadsheet
The saved results will also be displayed within a new spreadsheet window.
References
Bechhofer, R.E., Santner, T.J. and Goldsman, D.M. (1995). Design and Analysis of Experiments for Statistical Selection, Screening, and Multiple Comparisons. Wiley, New York.
Hsu, J.C. (1996). Multiple Comparisons Theory and Methods. Chapman & Hall, London.
(https://books.google.com/books?id=8AK8PUbw3lsC)
Maindonald, J.H. and Cox, N.R. (1984). Use of statistical evidence in some recent issues of DSIR agricultural journals. New Zealand Journal of Agricultural Research 27, 597-610.
Nelder, J.A. (1976). Discussion on papers by Wynn, Bloomfield, O’Neill and Wetherall. Journal of the Royal Statistical Society, Series B 33, 244-246.
Perry, J.N. (1986). Multiple-comparison procedures: a dissenting view. J. Econ. Entomol. 79, 1149-1155.
Bonferroni correction. https://en.wikipedia.org/wiki/Bonferroni_correction
Šidák correction. https://en.wikipedia.org/wiki/%C5%A0id%C3%A1k_correction
See also
- General Linear Regression
- Generalized Linear Models
- Predictions from General Linear Regression
- Predictions from Generalized Linear Model
- Multiple Comparisons dialog for ANOVA menus
- Multiple Comparisons for REML dialog
- MCOMPARISON procedure for all pairwise multiple comparison tests