1. Home
  2. Kernel Density Estimation
Searching...

Kernel Density Estimation

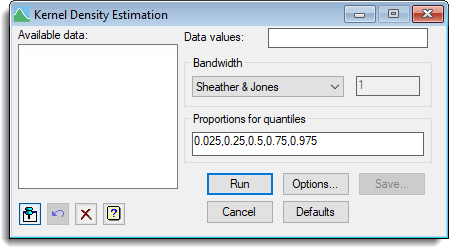
Select menu: Stats | Distributions | Kernel Density Estimation

Use this to evaluate a Kernel density estimate for a selected variate. A Kernel Density estimate can be thought of as a smoothed form of a histogram.

  1. After you have imported your data, from the menu select 
    Stats | Distributions | Kernel Density Estimation.
  2. Fill in the fields as required then click Run.

You can set additional Options then after running, you can save the results by clicking Store.

Kernel density estimation is a useful tool for exploring the unknown underlying distribution of a sample. The kernel method constructs an estimate fh(t) of the true density function by placing a kernel function K(t;xi,h) over each observation xi in the sample. The kernel function K(t;x,h) is itself a density function with location parameter x and scale parameter h, also called bandwidth in this context. The density estimate is then given by

	fh(t) = the sum of (K(t-xi)/h)/(nh) from i = 1...n

where n denotes the sample size. The choice of kernel function K is not very critical for the resulting estimate fh(t) and so a Gaussian kernel is used.

The following graph showing the sum of the normal kernels at 5 data points illustrates the ideas behind the kernel density estimation.

Bandwidth

The choice of bandwidth, h, is of crucial importance in kernel density estimation. A large value of h will give rise to an over smoothed density estimate, while a small value of h will produce a very ragged density with many spikes at the observations. It is recommended that a range of values of h be used, and the resulting kernel density estimates be examined, since this will highlight different features of the data.

For automatic use of kernel density estimation, estimation of the bandwidth h from the data is very helpful. The following automatic data driven estimates are available (n = the number of observations in the selected variate):

Sheather & Jones The method of Sheather & Jones (1991). Jones, Marron & Sheather (1996) recommend this for general purposes
Standard deviation s1 = 1.06 * (standard deviation) * n**(-1/5)
Interquartile range s2 = 0.79 * (inter quartile range) * n**(-1/5)
Min(Std Dev,IQ range) s3 = 0.90 * minimum(standard deviation, interquartile range/1.34) * n**(-1/5)
Given You provide your own estimate for the bandwidth in the associated field along side the dropdown list

The s1,s2 and s3 estimates of bandwidth are popular due to their simplicity and are optimal in some sense for data from a normal distribution.

Proportions for quantiles

Proportions at which to calculate quantiles of the kernel density estimate. This is either a comma or space separated list of numbers or may be the name of an existing variate.

Action buttons

Run Process the Kernel Density Estimation on the selected data.
Options Opens the Kernel Density Estimation Options dialog to allow various options to be set which control the output and graph.
Save Open the Kernel Density Estimation Save Options dialog to specify save structures for the analysis.
Cancel Close the dialog without running any more analyses.
Defaults Reset all options to their default values.

Action Icons

Pin Controls whether to keep the dialog open when you click Run. When the pin is down  the dialog will remain open, otherwise when the pin is up  the dialog will close.
Restore Restore names into edit fields and default settings.
Clear Clear all fields and list boxes.
Help Open the Help topic for this dialog.

See also

Updated on March 26, 2019

Was this article helpful?

Yes No