Select menu: Stats | Design | Generate a Standard Design
Use this to generate standard balanced factorial designs. You need to select the design type, name the treatment and layout factors and give the number of levels in each factor. When you click Run the design will be produced and randomized if required.
If the design is displayed in a spreadsheet the labels or numerical levels can be subsequently added to each factor using the options available from the Spread | Factor submenu.
- From the menu select
Stats | Design | Generate a Standard Design.
OR
Stats | Sample Size | Analysis of Variance. - Fill in the fields as required then click Run.
You can set additional options before generating the design by clicking Options.
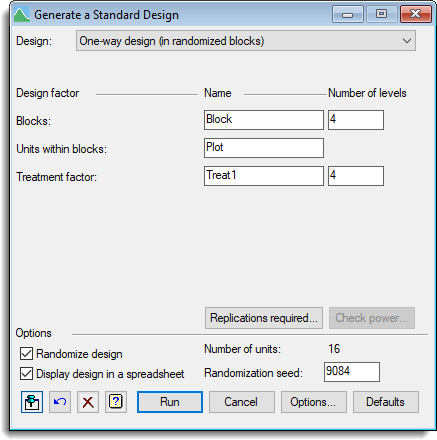
Design
This gives the available design types. These are:
One-way design (no blocking)
A single treatment factor is used and replicated a number of times with no restrictions on the treatment allocations to units.
One-way design (in randomized blocks)
A single treatment factor is used, replicated a number of times and arranged so that every treatment occurs once within a block of units.
Two-way design (no blocking)
Two treatment factors are used in a factorial arrangement (every combination of the two factors is used), and replicated a number of times with no restrictions on the treatment allocations to units.
Two-way design (in randomized blocks)
A factorial combination of two treatment factors is used, replicated a number of times and arranged so that every treatment occurs once within a block of units.
General treatment structure (no blocking)
Up to six treatment factors are used in a factorial arrangement (every combination of the factors is used) and replicated a number of times with no restrictions on the treatment allocations to units.
General treatment structure (in randomized blocks)
A factorial combination of up to six treatment factors is used, replicated a number of times and arranged so that every treatment combination occurs once within a block of units.
Completely randomized design
This is equivalent to the item General treatment structure (no blocking).
Split-plot design
A factorial combination of two treatment factors, arranged in replicates with the added restriction that one of the treatments is added to groups of units (the whole plots), then each level of the other factor is assigned within to units (the sub-plots) within the whole plots.
Split-split-plot design
A design with three levels of nesting of the allocation of three treatment factors. The main plot factor is allocated to whole plots. Within each whole plot, one of each level of the sub-plot factor is allocated to sub-plots. Within each sub-plot, one of each level of the sub-sub-plot factor is allocated to sub-sub-plots.
General split-plot design
A generalization of the split-plot design where factorial combinations of treatment factors can be allocated to either whole plots or sub-plots.
Strip-plot (or criss-cross) design
This generates a design for up to 4 treatment factors. The design is arranged in replicates, each of which consists of a row-by-column array of plots. All combinations of the levels of some of the treatment factors are applied to complete columns within each replicate, and all combinations of the other treatments are applied to complete rows within each replicate. (The design is thus similar to the general split-plot design, except that there are ‘whole plots’ running in two perpendicular directions.)
Latin square
A single treatment factor is allocated to a square arrangement of units such that each treatment occurs once within each row and column. The number of rows and columns therefore equals the number of treatment groups. The rows and columns may not present a spatial layout, but may be any pair of factors whose factorial combination divides the units into groups of size 1.
Graeco-Latin square
A Latin square with a second superimposed treatment factor so that every level of the new factor occurs once in each row and column, and every factorial combination of the two factors occurs once.
Square lattice design (blocks)
A spatial design where treatment levels are optimally allocated to blocks of plots within a replicate to minimize the confounding between the blocks and the treatment effects. The number of treatment levels must be a perfect square (e.g. 9,25,36,49…) and is equal to the square of the number of blocks within a replicate.
Lattice square design (rows and columns)
A spatial design where treatment levels are optimally allocated to rows and columns within a replicate. The number of treatment levels must be a perfect square (e.g. 9,25,36,49…) and is equal to the number of rows multiplied by the number of columns within a replicate.
Design factor
The various designs have factors that index the units and the applied treatments. These can be (depending on the design):
| Blocks | The factor that indexes the blocks in a randomized block trial. |
| Units | The factor that indexes the units within a trial with no blocking. |
| Units within blocks | The factor that indexes the units within blocks in a randomized block trial. |
| Treatment factor (1-5) | The factors (1-5) that index the factorial combination of treatments applied to the trial. |
| Whole plots | The factor that indexes the whole plots in a split-plot trial. |
| Sub-plots | The factor that indexes the sub-plots within whole plots in a split-plot trial. |
| Whole treat. factor (1-3) | The factors (1-3) that index the factorial combination of treatments applied to whole plots in a split-plot trial. |
| Sub-plot treat. factor (1-3) | The factors (1-3) that index the factorial combination of treatments applied to sub-plots in a split-plot trial. |
| Rows | The factor that indexes the rows in a strip-plot or Latin square trial. |
| Columns | The factor that indexes the columns in a strip-plot or Latin square trial. |
| Row treat. factor (1-3) | The factors (1-3) that index the factorial combination of treatments applied to rows in a strip-plot or Latin square trial. |
| Column treat. factor (1-3) | The factors (1-3) that index the factorial combination of treatments applied to columns in a strip-plot or Latin square trial. |
| Sub-sub-plots | The factor that indexes the sub-sub-plots within sub-plots in a split-split-plot trial. |
| Sub-sub-plot treat. factor | The factor that index the treatments applied to the sub-sub-plots in a split-split-plot trial. |
| Replicates | The factor indexes the replicates in a lattice design. |
No. of treatment factors
For designs where there are various number of treatment factors that can be handled, this specifies the number of treatments to be used in a factorial combination. This must be between 1 and 5.
No. of column treats
For a general strip-plot design, this specifies the number of treatment factors that are applied at the sub-plot level. This must be between 1 and the number of treatment factors − 1.
No. of sub-plot treats
For a general split-plot design, this specifies the number of treatment factors that are applied to the columns. This must be between 1 and the number of treatment factors − 1.
Name
The name to be used for each factor.
Number of levels
The number of classes or levels for each factor. For some designs the number may depend on other factors and in these cases the value will be displayed but cannot be changed.
Replications required
This opens a dialog that lets you calculate the number of replicates required to detect a response of a given size with a given probability of detection, variance parameters and confidence level. This is not available for Latin Square or Lattice designs, as the number of replicates in these designs is dependent on the number of levels of the treatment.
Check power
Lets you calculate the power for the chosen design, i.e. for a given level of response between two treatment groups and confidence level, it will calculate the probability of detecting this response. The current design must be generated with the Run button before this is enabled.
Randomize design
When selected, the design will be randomized, otherwise the units will be in standard order.
Display design in a spreadsheet
If this is selected, the resulting design will be put into a spreadsheet window. The resulting spreadsheet will contain all the statements required to analyse the results from the design using the Analyse Spreadsheet Columns menu. Also if you open the Stats | Analysis of Variance | General menu from the spreadsheet, then the TREATMENTS and BLOCKS items will be completed for you using the General Analysis of Variance design choice.
Number of units
This is an informational label indicating how many units the current design will have.
Randomization seed
This changes automatically every time a design is produced. If this is reset to a particular value used in a previous design, you will obtain the identical design a second time (i.e. units will have the same factor combinations). If providing your own seed, it should be a large integer (i.e. > 9999).
Action buttons
| Run | Generate the design. |
| Cancel | Close the dialog without further changes. |
| Options | Opens a dialog where additional options and settings can be specified for the designs. For example, the options include methods for modifying the basic designs (extra replication of a treatment, two way factorial combination with added control) and the form of unit labels generated (if the unit labels option is selected). |
| Defaults | Reset options to the default settings. Clicking the right mouse on this button produces a pop-up menu where you can choose to set the fields using the currently stored defaults or the Genstat default settings. |
Action Icons
| Pin | Controls whether to keep the dialog open when you click Run. When the pin is down |
|
| Restore | Restore names into edit fields and default settings. | |
| Clear | Clear all fields and list boxes. | |
| Help | Open the Help topic for this dialog. |
See also
- Replications required in a design
- Power for a design
- Generate a Standard Design Options
- Generate a Doubly Resolvable Row-Column Design menu
- Generate a factorial design in blocks menu for generating full factorial designs
- Generate a fractional factorial design menu for generating fractional factorial designs
- Generate a design efficient under ANCOVA menu
- Select design menu for a question and answer approach to creating a design
- Understanding factors within a spreadsheet
- Analyse Spreadsheet Columns
- General analysis of variance menu for analysing these designs using analysis of variance